[알고리즘] 정렬
비교 정렬 알고리즘
삽입정렬
삽입정렬 개념
두 번째 데이터부터 시작해서 마지막 데이터까지 비교한다.
선택된 자료의 왼쪽 데이터들과 비교하여 선택된 자료의 크기가 작다면 자리를 바꾼다.

삽입정렬 코드
두 번째 데이터부터 시작해서 마지막 데이터까지 돌아가며 비교
// 정렬된 부분과 정렬되지 않은 부분으로 나누어 정렬
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
// key보다 큰 원소들을 한 칸씩 뒤로 이동
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}삽입정렬 시간복잡도
- Best Case
데이터가 이미 정렬되어 있을 때 최적의 경우이다.
시간 복잡도 : O(1) - Worst Case
데이터가 역순으로 정렬되어 있을 때 최악의 경우다.
시간 복잡도 : O(n^2)
분할정복(divide and conquer) 알고리즘
분할정복 개념
작은 문제로 분할하여 문제를 해결하는 방법이다.
분할정복를 사용하는 정렬 알고리즘으로는 퀵 정렬, 합병 정렬, 이진 탐색 등이 있다.
분할정복 설계
1. Divide
원래 문제를 여러 sub 문제로 분할
2. Conquer
재귀적으로 분할한 문제를 해결함(ex, 정렬)
3. Combine
Conquer이 완료된 문제들을 다시 합쳐서 원래 문제와 같은 형태로 만듬

합병정렬(분할정복 기반 O(nlgn))
합병정렬 개념
분할정복 알고리즘을 기반으로 하는 정렬 알고리즘이다.
하나의 큰 문제를 2개의 문제로 재귀적으로 계속해서 나누고 정렬한 후 다시 합치는 방식이다.
1. 분할(Divide)
더 이상 나눌 수 없을 때까지 두 개의 subarrays로 나눔
A[p
r] -> A[p
q] & A[q+1 ~ r]
2. 정복(Conquer)
3. 결합(Combine)

합병정렬 코드
public class SortingAlgorithms {
// 배열을 반으로 나누고, 정렬 후 합병하는 분할 정복 방식
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
// 중간 지점 계산
int mid = (left + right) / 2;
// 왼쪽 절반 정렬
mergeSort(arr, left, mid);
// 오른쪽 절반 정렬
mergeSort(arr, mid + 1, right);
// 정렬된 두 절반을 합병
merge(arr, left, mid, right);
}
}
// 합병 함수
private static void merge(int[] arr, int left, int mid, int right) {
// 두 부분 배열의 크기 계산
int n1 = mid - left + 1;
int n2 = right - mid;
// 임시 배열 생성
int[] L = new int[n1];
int[] R = new int[n2];
// 데이터를 임시 배열로 복사
for (int i = 0; i < n1; ++i)
L[i] = arr[left + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[mid + 1 + j];
// 두 임시 배열을 합병
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// L[]의 남은 요소들을 복사
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// R[]의 남은 요소들을 복사
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 테스트를 위한 메인 메소드
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
int[] arrForMergeSort = arr.clone();
mergeSort(arrForMergeSort, 0, arrForMergeSort.length - 1);
}
}합병정렬 시간복잡도
Best Case와 Worst Case 모두 O(nlogn)이다.

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
버블정렬
버블정렬 개념
서로 인접한 두 원소를 검사하여 정렬한다.
첫 번째 : 두 번째 / 두 번째 : 세 번째 /.../ 마지막-1 : 마지막까지 비교하는 작업을 수행하면 가장 큰 자료가 맨 뒤에 이동된다.
이 작업을 n-1번 반복한다.(크기 : n)
이렇게 순차적으로 한 번의 자리 교체가 완료되면, 가장 큰 수가 배열의 가장 뒤로 보내진다.

버블정렬 코드
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n-1; i++)
for (int j = 0; j < n-i-1; j++)
// 인접한 두 원소를 비교하여 큰 수를 뒤로 이동
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}버블정렬 시간복잡도
Best Case와 Worst Case 모두 O(nlogn)이다.
버블정렬 Loop Invariant 증명

배열 : A[p~r]
j : 피봇과 비교하기 위해 선택된 원소
i : 파티션 바로 뒤 원소
- A[j]와 피봇을 비교
- if A[j]가 피봇보다 작다면 A[i]와 위치를 바꾸고 i을 한 칸 앞으로 옮김으로써 파티션을 한 칸 앞으로 옮김
else A[j]가 피봇보다 크다면 for 반복문 그대로 실행(j 다음 원소와 피봇을 비교)

- 초기 조건
- 루프 시작 전 A[p~i], A[i+1 ~ j-1]은 모두 비어 있으므로 루프 불변성을 만족한다.
- 유지 조건
- 루프가 도는 동안
- if A[j]가 피봇보다 작거나 같다면 A[j], A[i+1]를 바꾸고 i와 j는 증가한다.
- if A[j]가 피봇보다 크다면 j만 증가한다.
- 종료 조건
만약 j==r이라면(마지막에 도달했다면) A[pi]는 피봇보다 작은 서브 배열이고 A[i+1r-1]는 피봇보다 큰 서브 배열이고 A[r]은 피봇이 되므로 버블 정렬이 완성된다.
https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
힙정렬(O(nlgn))
힙 개념
- 힙 높이 : O(logn)
h : 높이
n : 노드 개수

- 부모 - 자식( A[1 ~ n] )
- Root of tree is A[1].
- Parent of A[i ] = A[i/2].
- Left child of A[i ] = A[2i ].
- Right child of A[i ] = A[2i + 1]

- 힙은 이진 트리가 아닌 k-ary 트리도 사용 가능하다(4진, 8진, 16진 트리 등)
Max Heap vs Min Heap
힙 정렬에는 Max Heap만을 사용한다! Min Heap 사용하지 X

Max Heap(Heap 정렬에 사용)
부모 노드가 자식 노드보다 크거나 같은 경우(부모 => 자식)
즉, root 값이 가장 크고 내려올 수록 작아짐
A[PARENT(i )] ≥ A[i]

Min Heap
부모 노드가 자식 노드보다 작거나 같은 경우(부모 <= 자식)
즉, root 값이 가장 작고 내려올 수록 커짐
A[PARENT(i )] ≤ A[i]

Max-Heapify(하향식)
왼쪽 자식 트리와 오른쪽 자식 트리가 모두 Heap 속성을 만족하는데 root 노드만 만족하지 않는 경우
즉, root 노드가 왼쪽 자식 노드 or 오른쪽 자식 노드보다 작은 경우 재정렬을 통해 Heap 속성을 만족시키게 하는 연산
or
배열의 첫번째인 부모 노드부터 시작하여(주로 root부터) 배열의 끝으로 내려가며 max heap을 만드는 하향식 방법
(둘 중 뭐가 맞는지 모르겠는데 일단 둘 다 알아두기)

root 노드와 두 자식 노드를 비교하고 두 자식 노드 중 더 큰 노드와 root 노드의 자리를 바꾼다.
이 작업을 반복하여 자식 노드보다 크거나 마지막 level까지 갔을 때 중단한다.


Max-Heapify 코드

Build Max Heap(상향식)
배열의 끝에서부터 시작하여 root로 올라가며 max heap을 만드는 상향식 방법

Build Max Heap 코드 및 시간복잡도
시간복잡도 : O(nlogn)
MAX-HEAPIFY가 O(logn)이고 이 작업을 n번 하므로 O(nlogn)
BUILD-MAX-HEAP
heap-size[A]<-length[A]
for i <- |length[A]/2| downto 1
do MAX-HEAPIFY(A,i)우선 순위 큐 이용한 힙 정렬
- Linked-List를 이용한 힙 정렬 시간 복잡도
- 삽입 연산 : O(n)
- 삭제 연산 : O(1)
- 우선순위 큐를 이용한 힙 정렬 시간 복잡도
- 삽입 연산 : O(logn)
- 삭제 연산 : O(logn)
결과적으로 우선 순위 큐를 이용한 힙 정렬 삽입/삭제 연산의 시간 복잡도가 더 빠르다.
Heap-Increase-Key(노드 값 변경)
원래 노드(i)를 key 값으로 변경하는 연산

A[i] == 4인 노드를 15로 변경하고 힙 정렬

- 시간 복잡도
- O(logn)
최댓값 삭제 연산(마지막 노드를 root 노드로 이동한 후 힙 연산)

- root 노드를 삭제하고 마지막 노드를 root로 이동한다

- 힙 정렬


- 코드

- 시간 복잡도
- O(logn)
https://dev-ku.tistory.com/249
최댓값 삽입 연산(마지막 노드에 삽입 후 힙 연산)
- 새로운 값을 마지막 노드에 삽입
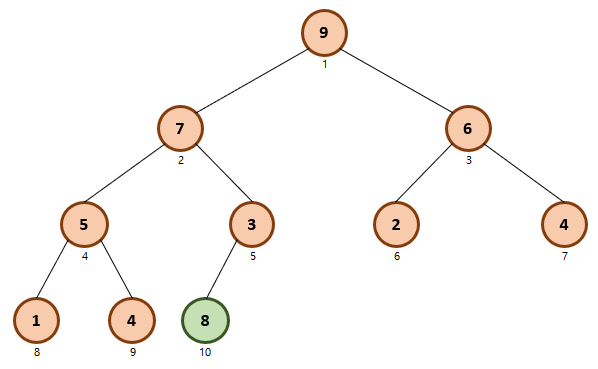
- 부모 노드와 비교해가며 힙 정렬 수행


- 코드

https://johoonday.tistory.com/129
힙정렬 시간복잡도
Best Case와 Worst Case 모두 O(nlogn)이다.
https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
https://rninche01.tistory.com/entry/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-04-%ED%9E%99-%EC%A0%95%EB%A0%AC
퀵정렬(분할정복 기반 / 피벗, 칸막이)
퀵정렬 개념
하나의 리스트를 피벗(pivot)을 기준으로 두 개의 부분리스트로 나누어 하나는 피벗보다 작은 값들의 부분리스트, 다른 하나는 피벗보다 큰 값들의 부분리스트로 정렬한 다음, 각 부분리스트에 대해 다시 위 처럼 재귀적으로 수행하여 정렬하는 방법이다.
분할 정복 알고리즘을 기반으로 정렬되는 방식으로써 병합 정렬과 유사하지만 명확한 차이가 있다.
- 병합 정렬 vs 퀵 정렬
- 병합 정렬
- 하나의 리스트를 왼쪽, 오른쪽 절반으로 나누어 정렬한다.
- 퀵 정렬
- 피벗을 기준으로 피벗보다 작은 부분, 피벗보다 큰 부분으로 나누어 정렬한다.
- 부분 리스트의 크기가 병합 정렬과 다르게 비균등하게 나뉠 수 있다.퀵정렬 코드
- 병합 정렬
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi-1);
quickSort(arr, pi+1, high);
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = (low-1);
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1;
}퀵정렬 시간복잡도
- Best, Average Case - O(nlgn)
- Worst Case - O(n^2)
이미 정렬이 되어 있는 경우 최악의 효율(정렬, 역정렬)
ex. 1, 2, 3, 4, 5, ... , n 또는 n ... , 5, 4, 3, 2, 1
https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
선형 시간 복잡도 정렬 알고리즘(카운팅, 기수, 버킷 - O(n))
카운팅 정렬(계수 정렬)
계수 정렬은 대소를 비교하여 정렬하는 알고리즘이 아니다. 시간 복잡도는 O(n)으로 비교 알고리즘보다 빠르다. 하지만 실제 시간 복잡도는 O() + k)이므로 정렬하려는 대상에 따라서 시간 복잡도가 엄청나게 커질 수도 있다.
카운팅 정렬 원리

- 카운팅 배열을 만든다.
위 배열에 있는 값을 index로 하는 배열을 만든다.
즉, 1, 2, 3, 4의 값이 존재하니깐 index가 1,2,3,4인 배열을 만든다.

- 카운팅 배열에 요소의 개수를 넣는다.
1은 2개, 2는 3개, 3은 1개, 4는 2개 존재 -> 카운팅 배열에 2, 3, 1, 2 넣기

- 누적합 배열을 만든다.
카운팅 배열을 누적합 배열로 만든다.
즉, index가 2인 요소는 index2 = index1, 2 / index3 = index1, 2, 3 / index4 = index1, 2, 3, 4 ...

- 누적합 배열을 순회하 정렬 배열을 만든다.
index 값을 요소 수만큼 배열에 넣어서 정렬된 배열을 만든다.

https://bamtory29.tistory.com/entry/%EC%B9%B4%EC%9A%B4%ED%8C%85-%EC%A0%95%EB%A0%AC
카운팅 정렬 시간 복잡도
- 카운트 배열
정렬되지 않은 배열을 쭉 돌면서 해당 값이 몇 개 있는지 확인만하면 되니깐 O(n) - 누적합 배열
카운트 배열을 쭉 돌면서 앞 요소 값 + 현재 요소 값을 하면 되니깐 O(n) - 정렬된 배열
누적 합 배열을 순회하면서 정렬된 배열을 만들면 되니깐 O(n)
결국 카운팅 정렬의 시간 복잡도는 O(n)이 되는 것이다 !!
카운팅 배열의 한계(단점)
- 값의 범위가 너무 크지 않아야 한다.(메모리 사이즈를 넘기면 안된다.)
카운팅 배열은 요소의 값을 index로 저장한다.
1, 3, 5, 45, 167 값이 있고 각 값이 2개 or 3개씩만 있다고 가정해보자
최대 15개의 값이 존재하지만 각 요소의 값을 index로 저장하기 때문에 배열의 크기는 array[168]이 된다.
15개의 요소만 존재하지만 168의 배열을 만들어야 하므로 엄청난 메모리 낭비가 발생한다.
- 데이터(값)은 양수여야 한다.
값을 배열의 index로 저장해야 하는데 index가 음수일 수 없으니 양수만 가능하다.
더 구체적인 예시를 보고 싶다면
https://velog.io/@chappi/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-6%EC%9D%BC%EC%B0%A8-On-%EC%A0%95%EB%A0%AC-%EA%B3%84%EC%88%98-%EC%A0%95%EB%A0%AC
기수 정렬(Radix Sort)
각 수들의 자리수 별로 정렬하는 방법이다.

각 자리수별로 정렬하면 최종적으로는 완벽하게 정렬된 배열이 나온다.
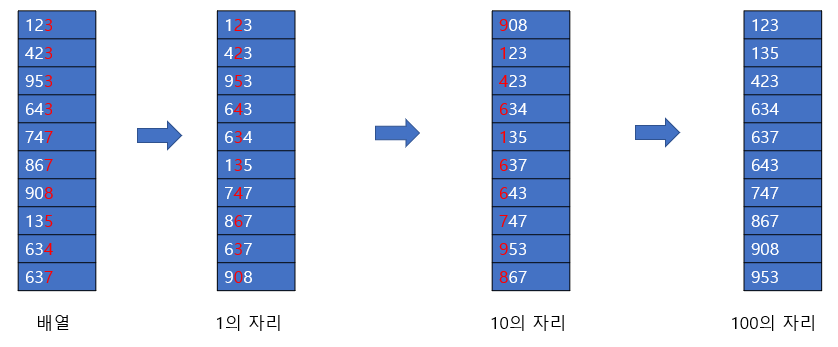
왜 1의 자리부터 정렬해야 할까?
예를 들어 124, 123, 115가 있다고 가정해보자. 그리고 100의 자리 -> 10의 자리 -> 1의 자리 순서로 정렬해보자.
- 100의 자리
124, 123, 115 - 10의 자리
115, 124, 123 <- 순서가 뒤바뀜 - 1의 자리
123, 124, 115 <- - 순서가 뒤바뀐다.
즉, 작은 자리 수부터 정렬하는 이유는 앞에서 정렬한 원래 순서를 유지하기 위함이다.
버킷 정렬
- 데이터들을 나눌 수 있게 버킷을 만든다.(ex. 가장 큰 자리 수(0~9)
- 데이터들을 버킷에 나눠 담는다.
- 각 버킷안에 있는 데이터들을 정렬한다.(이때 사용하는 정렬 알고리즘은 사용자 맘대로 사용)
- 버킷 내부의 정렬된 값들을 하나로 이어서 정렬된 배열을 만든다.

기수 정렬 vs 버킷 정렬
- 기수 정렬
각 자릿수별로 정렬을 진행하는 것 - 버킷 정렬
크게 나눌 수 있는 카테고리로 버킷을 구분(여기까진 기수 정렬과 비슷)
이후 각 버킷별로 정렬 실행 후 모든 버킷을 하나의 정렬로 만들어서 하나의 정렬된 배열을 만듬(이부분이 차이점)