문제

나무 자르기

문제 해설

아래 그림처럼 나무(L)의 높이(H)에서 자르면 L-H길이 만큼 가져갈 수 있다.

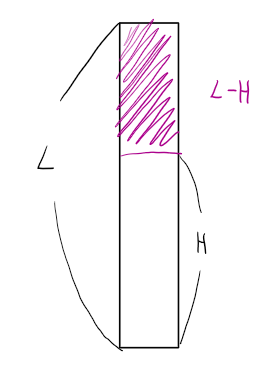
low, high, mid 설정
- low와 high는 최소 높이(1)와 최대 높이(가장 큰 나무)로 설정한다.
- mid는 나무를 자르는 높이로 설정한다.
풀이 방법
1. 나무를 순회하며 mid 높이만큼 자르고 가져간 나무를 카운팅한다.
2. 가져갈 수 있는 나무와 가져가려고 하는 나무를 비교하여 이분 탐색을 진행한다.
  - 가져갈 수 있는 나무 >= 가져가려고 하는 나무: 높이의 최대 값을 구해야 하기 때문에 mid를 높이기 위해 오른쪽을 탐색(low = mid + 1)한다.
  - 가져갈 수 있는 나무 < 가져가려고 하는 나무: 왼쪽을 탐색(high = mid - 1)한다.

package BinarySearch;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class _2805_나무_자르기 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken()); // 나무의 수
        int m = Integer.parseInt(st.nextToken()); // 필요한 나무 길이

        int[] trees = new int[n];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < n; i++)
            trees[i] = Integer.parseInt(st.nextToken());

        Arrays.sort(trees);

        int low = 0;
        int high = trees[n-1];
//        int result = 0;
        while (low <= high) {
            int mid = (low + high) / 2;

            // 1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000 조건이 주어졌다. 따라서 sum이 int 범위를 넘어설 수 있어서 long으로 설정
            long sum = 0;
            for (int tree : trees) {
                if (tree > mid) {
                    sum += tree - mid;
                }
            }
            if (sum >= m) {
//                result = mid;
                low = mid + 1;
            } else {
                high = mid - 1;
            }

             /*문제의 목표는 나무의 길이가 딱 m인 값을 찾는 게 아닌 m에 가까운 최적의 값을 찾는 것임
             문제에서 sum == m이 반드시 있을 거란 보장이 없음
             예를 들어, 특정 톱 높이에서는 sum > m이고, 그 다음으로 작은 톱 높이에서는 sum < m이 되는 경우가 있을 수 있음
             따라서 최대한 m에 가깝게 나무를 자르는 최적의 높이 찾기 위해 위 코드를 사용함.
            if (sum == m) break;
            else if (sum > m) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }*/
        }
        // sum == mid일 때 low = mid + 1이 된다.
        // low가 커지면 mid도 커지고 sum이 작아질 수 밖에 없음
        // sum이 작아지면 high = mid -1이 되고 결과적으로 low > high 상황이 발생함.
        // 이때 low = 최적 값 +1이고 high = 최적 값이 된다.
        // 따라서 high(최적 값)을 출력함.
        /* 예시
        low / mid / high
        36 / 36 / 37 -> sum == m
        37 / 37 / 37 -> sum < m
        37 / mid / 36 -> low > high 발생 -> 탈출
        결과: high == 최적값
        */
        System.out.println(high);
    }
}