[백준] 11725 트리의 부모 찾기(Silver.2) - DFS

문제

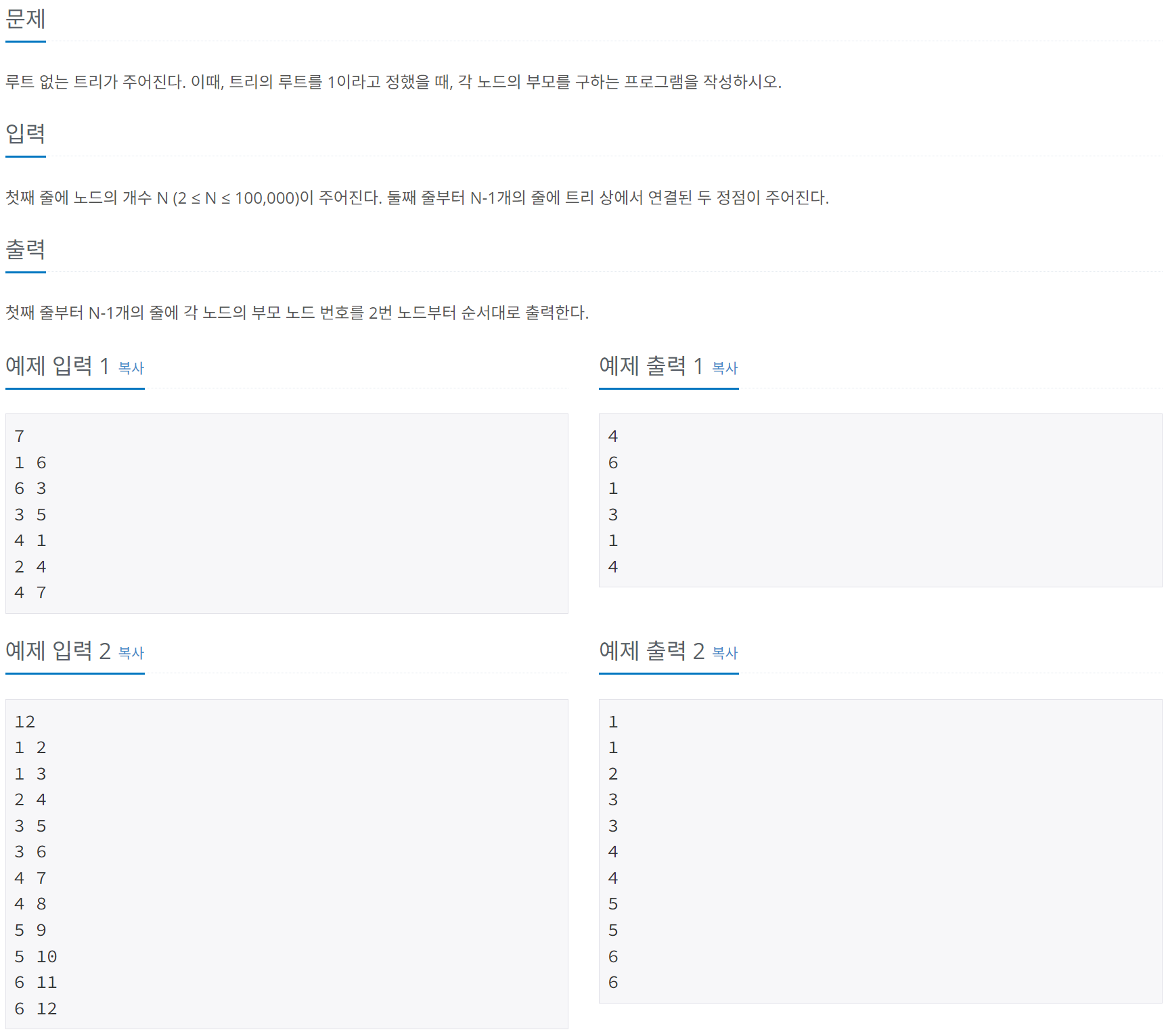
코드

• 풀이 방법

1. 연결 리스트 형태로 그래프 구현
2. 루트인 1부터 깊이 우선 탐색 진행
   • 아래 사진처럼 1 노드부터 시작하여 자식 노드로 내려가면서 깊이 우선 탐색을 진행한다.

3. 깊이 우선 탐색을 진행하며 배열에 노드의 부모 노드를 저장한다.

4. 부모 노드가 저장된 배열을 2번부터 N번까지 출력한다.

• LinkedList 사용

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.StringTokenizer;

public class _11725 {
    static LinkedList<Integer>[] graph;
    static boolean[] visited;
    static int[] parents;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());
        graph = new LinkedList[N+1];
        parents = new int[N+1];
        visited = new boolean[N+1];

        for (int i = 1; i <= N; i++)
            graph[i] = new LinkedList<>();

        for (int i = 0; i < N-1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            graph[a].add(b);
            graph[b].add(a);
        }

        dfs(1);
        for (int i = 2; i <= N; i++)
            System.out.println(parents[i]);
    }
    public static void dfs(int nowNode) {
        visited[nowNode] = true;

        for (int node : graph[nowNode]) {
            if (!visited[node]) {
                parents[node] = nowNode;
                dfs(node);
            }
        }
    }
}

• ArrayList 사용

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.ArrayList;

public class _11725 {
    static ArrayList<Integer>[] graph;
    static boolean[] visited;
    static int[] parents;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());
        graph = new ArrayList[N+1];
        parents = new int[N+1];
        visited = new boolean[N+1];

        for (int i = 1; i <= N; i++)
            graph[i] = new ArrayList<>();

        for (int i = 0; i < N-1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            graph[a].add(b);
            graph[b].add(a);
        }

        dfs(1);
        for (int i = 2; i <= N; i++)
            System.out.println(parents[i]);
    }
    public static void dfs(int nowNode) {
        visited[nowNode] = true;

        for (int node : graph[nowNode]) {
            if (!visited[node]) {
                parents[node] = nowNode;
                dfs(node);
            }
        }
    }
}