문제

풀이 방법

타겟 넘버 문제는 모든 경우의 수를 구하는 문제이고 총 2^numbers.length의 경우의 수가 존재한다.

이 문제는 DFS와 BFS로 풀 수 있는데 2^numbers.length가지 경우를 모두 탐색해야 하므로 두 알고리즘 모두 시간 복잡도는 O(2^numbers.length)으로 같다.

하지만 DFS는 깊이에 비례하며 공간 복잡도가 O(numbers.length)인 반면 BFS는 중간 결과값까지 모두 큐에 저장해야 하므로 최악의 경우 공간 복잡도는 O(2^numbers.length)이 될 수 있다.

따라서 이 문제와 같이 깊이(numbers의 크기)가 정해져 있고 너비가 깊이에 따라 지수적으로 증가하는 문제는 메모리 효율성 측면에서 DFS가 BFS보다 효율적이다.

BFS

numbers 배열의 값을 순환하며 더하고 뺀 값을 큐에 삽입하는 방식으로 BFS를 구현했다. 모든 경우의 수를 구해야 하기 때문에 방문 여부는 체크하지 않았다.

큐(Queue)
- {현재 값, 레벨}

풀이 방법

큐를 선언하고 numbers의 '+첫 번째 값'과 '-첫 번째 값'과 레벨을 삽입한다.

// {현재 값, 레벨}
Queue<int[]> q = new LinkedList<>();
q.offer(new int[] {numbers[0], 0});
q.offer(new int[] {-numbers[0], 0});

큐에서 뺀 값이 조합이 완료된 값이고 목표 값과 동일하다면 카운팅을 한다.

int[] current = q.poll();
int cLevel = current[1]+1;
if (cLevel == numbers.length && current[0] == target) cnt++;

큐에서 현재 값을 빼고 현재 값에 numbers[index+1]를 index+1가 범위 내라면 더한 값과 뺀 값이 큐에 삽입한다.

if (cLevel < numbers.length) {
    q.offer(new int[]{current[0] + numbers[cLevel], cLevel});
    q.offer(new int[]{current[0] - numbers[cLevel], cLevel});
}

numbers = [4, 1, 2, 1]인 값을 조합하면 아래 사진과 같이 조합된다.

BFS 코드

import java.util.*;

class Solution {
    public int solution(int[] numbers, int target) {
        return bfs(numbers, target);
    }

    public int bfs(int[] numbers, int target) {
        // {현재 값, 레벨}
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[] {numbers[0], 0});
        q.offer(new int[] {-numbers[0], 0});

        int cnt = 0;
        while (!q.isEmpty()) {
            int[] current = q.poll();
            int cLevel = current[1]+1;
            if (cLevel == numbers.length && current[0] == target) cnt++;
            if (cLevel < numbers.length) {
                q.offer(new int[]{current[0] + numbers[cLevel], cLevel});
                q.offer(new int[]{current[0] - numbers[cLevel], cLevel});
            }
        }
        return cnt;
    }
}

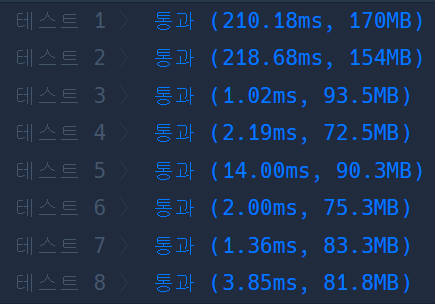
DFS에 비해 메모리도 많이 사용하지만 시간이 매우 오래 걸린다.

이는 큐에서 poll()하고 add()하는 과정과 큐에 저장할 객체(int[] {index, value})를 생성하는 과정에서 지속적인 오버헤드가 생기기 때문이다.
함수 호출만을 사용하는 DFS의 코드를 보자.

DFS

class Solution {
    int result = 0;

    public void dfs(int sum, int[] numbers, int target, int cnt) {
        // 마지막 값까지 합쳐졌을 때만 target 값과 비교하도록 조건문 설정
        if (cnt == numbers.length) {
            if (sum == target) {
                result++;
                // 여기 return을 설정해놔서 오류가 났고 해결하지 못했음
            }
            return;
        }
        // +, - 각각 호출
        dfs(sum +numbers[cnt], numbers, target, cnt+1);
        dfs(sum -numbers[cnt], numbers, target, cnt+1);
    }

    public int solution(int[] numbers, int target) {

        // dfs()를 +, - 각각 두 번 호출한다.
        dfs(0, numbers, target, 0);
        return result;
    }
}

큐에 값을 넣거나 빼지도 않고 객체를 생성할 필요도 없기 때문에 BFS에 비해 매우 빠른 것을 볼 수 있다.